みなさんは、数字に対してどのようなイメージがあるでしょうか。
仕事に必要なツールとしてはもちろんですが、コンピュータの世界では当たり前のように利用されている数字。
今回は、学校ではなかなか教えてくれないコンピュータの世界における数学について示していきたいと思います。いわばプログラマーに必要な数学の基礎といったところですね。
数字の数え方について
「10」
これ、何て読みますか?候補としては「じゅう」「とお」「いちぜろ」等ですかね。
実は、どの読み方も正解です。
私たちは、文字や画像を別のものとして扱えますが、コンピュータはこれら全てを「0」と「1」に置き換えて処理します。
人とコンピュータの最大の違いといっても過言ではありません。
与えられた情報をどう扱うのか、そのために情報をどうやってコンピュータに伝えるのか、これらは人間が決めることです。
まずは、人がコンピュータと同じ方法で数を数えられるようになる必要があるってことです。
位取り記数法
位取り記数法は、数値の書き表し方のことです。私たちが日常で使っているのは10進法になり、コンピュータが使うのは2進法です。
他にも8進法や16進法など、数値を表現する方法はたくさんあります。
同じ数値でも、位取り記数法が異なれば、違う値で表記されることになります。
普段生活の中で使っている10進法は、0~9の10種類の数字を使い、数字の桁は右側から順に1の位、10の位、100の位・・・といった感じで表します。
10進法の「10」は、使用できる数字の種類を表していると覚えておけば良いです。
2進数や16進数も、使用する数字の種類と各桁の表す意味がそれぞれ異なるだけで、数え方のルールは基本的に同じです。
その桁で使える数字を使いきったら、桁が繰り上がります。これが位取り記数法ですね。
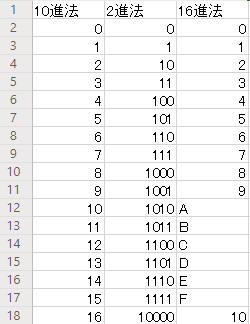
10進法、2進法、16進法をそれぞれ表現するとこの画像のようになります。
16進法はやや特殊で、0~9の10種類の数字と、A~Fの6種類のアルファベットを合わせて16種類の文字で数を表します。
1桁で2進数の4桁分を表せるので、16進数は桁が大きくなりがちな2進数を効率よく表現するために使われますね。とてもハイスペックです。
「0」の役割について
パソコンをよく使う人なら、ビットやバイトという言葉を聞いたことがあると思います。
ビットはコンピュータが扱う最小単位で、2進数の1桁に相当します。
一方バイトは、ビットが8個集まったもので、ファイルのサイズやHDDの容量を表す際によく使いますね。KB(キロバイト)やGB(ギガバイト)など、バイトはコンピュータが情報を読み書きするときの基本単位になります。
8ビットで1バイトになり、ビット単位で読み書きすることはないので、2進数「11000」といった値を8ビットで表す場合は、左側に0を付け足して「00011000」と表現します。
右側に0を付け足してしまうと、全く別の値になってしまうので間違えないようにします。
「0」って意味がなさそうに見えて、物凄く意味のある数字なんです。
基数変換
基数変換とは、表記されている数値を別の位取り記数法に変換することです。
例えば、10進数の「1992」という値。
- 1000が1つ
- 100が9つ
- 10が9つ
- 1が2つ
これらの値を全部足したものになります。
1000や100など各桁に意味を持たせている値を「重み」と言います。
(10³×1)+(10²×9)+(10¹×9)+(10⁰×2)
数式に直すと気づくと思いますが、全ての桁の重みが「10のn乗」で表していますね。
指数は右から順に1つずつ増えています。桁が繰り上がるたびに重みの値も大きくなります。
重みの基本になる「10」ですが、これは10進数の「10」のことです。2進数なら「2」が、16進数ならば「16」が基本になります。この値を「基数」や「底」と呼びます。
2進数から10進数に
基数が分かったところで、2進数から10進数に変換してみます。
例として「11000」という値を数式に直してみます。
(2⁴×1)+(2³×1)+(2²×0)+(2¹×0)+(2⁰×0)=24
となり、10進数の「24」になります。
10進数から2進数に
先ほど例としてあげた「1992」という値について考えてみます。
1000の位が「1」、100の位が「9」、10の位が「9」、1の位が「2」ですよね。
これらの値は、基数で繰り返して割り算したときの余りになります。
つまり、10進数の基数は10なので、1992を10で割り続けて商が0になるまで繰り返すと、各桁の値を表すことが出来ます。
1992÷10=199・・・2
199÷10=19・・・9
19÷10=1・・・9
1÷10=0・・・1
下から順番に並べると、元の値に戻りましたね。
これと同様に、10進法で表記された数値を2進数に変換します。
2進数に変換したいので、2進数の基数である「2」で割り算していきます。そして商が0になるまで繰り返せば2進数になります。
例として「50」を2進数にします。
50÷2=25・・・0
25÷2=12・・・1
12÷2=6・・・0
6÷2=3・・・0
3÷2=1・・・1
1÷2=0・・・1
下から順に並べると「110010」になります。
10進数から16進数に
10進数の数値を16進数に変換する場合は、元の値を「16」で割り算すればOK。
アルファベットが混ざるので若干ややこしい部分がありますが、基本は同じです。
例として「60」を16進数にしてみます。
60÷16=3・・・12
3÷16=0・・・3
そのまま並べると「312」になっちゃうので注意。「12」は16進数だと「C」と表現するのでこの場合は「3C」となります。
2進数から16進数に
16進法では、0~9及びA~Fの16種類の文字や数字を使うんでしたよね。これは、2進法の4桁分に相当します。
2進数を16進法の表記に変換するときは、右側から4桁ずつ区切って、それぞれを16進法の値に置き換えていきます。
例として「11100」を16進数にしてみます。
まずは、8桁になるように、左側に0を付け足して「00011100」とします。
次に、右側から4桁ずつ分けて「0001」と「1100」にします。
「0001」は「1」、「1100」は「C」になるので16進法で「1C」となります。






