キャラクターが動かせるようになりボールも落ちてくるようになって、とてもゲームっぽくなってきました。
しかし、このままだと当たり判定がなくボールがキャラクターに当たったことを感知することが出来ません。ゲームっぽいですが、まだゲームとして成り立っていないわけですね。
というわけで、今回は当たり判定を実装していきたいと思います。
当たり判定を実装する
そもそも、当たり判定とはオブジェクト同士が衝突したことを検出するための仕組みのことです。
現在の状態だと、当たり判定を実装していないので、キャラクターとアイテムが衝突してもすっと下にすり抜けてしまいます。
この状態を防ぐためにも、オブジェクト同士の衝突をチェックしておき、衝突した場合には何かしらの処理を行うようにします。
当たり判定の簡素化
キャラクターに猫を使っているので、本格的な当たり判定を実装しようとすると、非常にスクリプトが複雑になります。
というもの猫には両耳があるので、その部分に降ってきたボールが接しているのかどうかを判定しようとすると計算量が膨大になってしまいます。
ですから、もう少し簡単な方法を考えないといけません。
どうするのかというと、猫の形状を円形と捉えることで円の中心座標と半径さえわかれば当たり判定を実装することが出来ます。

イメージとしてはこんな感じです。オレンジの枠内にボールがひっかかると当たり判定になります。
ここまでは簡単ですが、ここからが数学の知識が問われる茨の道になってきます・・・。
三平方の定理について
今回、スクリプトを実装するにあたって避けては通れないものが数学の知識です。
直角三角形の2辺の長さが分かれば残りの1辺の長さも分かってしまうという「三平方の定理」を使う事になります。
降ってくるボールの半径を「r1」、猫を囲んだ円の半径を「r2」にします。そして、それぞれの中心座標を「p1」と「p2」にします。
これで、三平方の定理を使ってボールの円の中心と猫の円の中心の距離を求めることが出来ます。
公式にあてはめると、d(距離)=√(p1x – p2x)²+(p1y – p2y)²ですね。
2つの円の中心の距離dが「r1+r2」よりも大きければ、2つの円は衝突していないことになります。逆に小さい場合は衝突します。
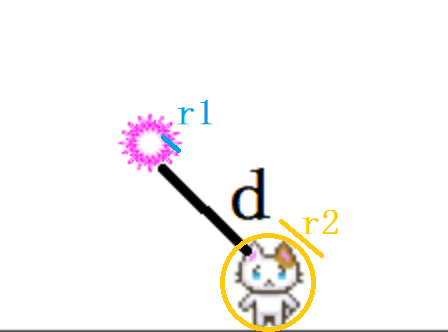
図にするとこんな感じです。ボールが近づいてくるとdの距離が小さくなるので、衝突条件を満たすわけですね。
このような処理をスクリプトにしていきます。
当たり判定のスクリプトの作成
以前作成しておいたボールのスクリプトを修正していきます。
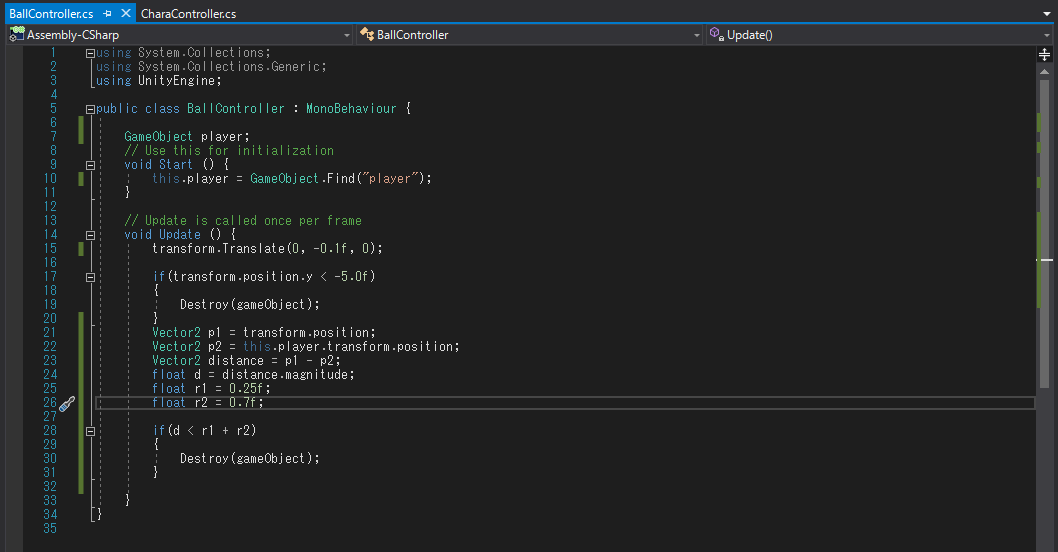
まずは、猫のオブジェクトを呼び込まないといけないので猫オブジェクトを追加しておきます。
肝心の当たり判定ですが、21行以降ですね。
先ほど三平方の定理に当てはめたp1やr1などをそのまま変数として使っています。座標に関してはベクトルを求める必要があるのでVector2型になります。
21行目と22行目で、自分自身と猫の座標をそれぞれ代入しています。
次に、23行目でp2からp1に向かうベクトルを求めます。
dの距離は、Vector2クラスのmagnitude変数を使う事で求める事が出来ます。ベクトルの長さがそのまま距離になるわけです。
25行目と26行目でそれぞれのオブジェクトの半径の値を指定します。
最後に、2つのオブジェクトの距離が「r1+r2」以下になった場合は衝突したと判断しDestroyメソッドでボールオブジェクトを破棄します。
これで、当たり判定が実装されました。実際にゲームを実行してみると、ボールが猫に衝突したらちゃんとボールが消えることを確認できました。
思った以上に早く消える場合や、消えるのが遅い場合は、オブジェクトの半径の値を確認して調整するようにします。
このままだと、ゲーム開始時にボールが1個しか降ってきませんので避けるのもとても簡単です。
次の作業は、ボールを量産してゲームの難易度を高めていきたいと思います。今回はこの辺で。






